Contour Integrals
A contour integral is essentially a line integral in the complex plane.
Given a smooth curve $C$ in a domain $D$ and $f(z) = u(x,y) + v(x,y)i$ a continuous function defined along $C$, we say that
$$ \int_{C} f(z) dz = \int_C (u+vi)(dx + dyi) = \int_C ( u dx - vdy ) + i \int_C (vdx + udy). $$
We can parameterize $C$ as
$$ C : z = z(t) = x(t) + y(t)i, \quad \alpha \le t \le \beta $$
Then, $z'(t) = x'(t) + i y'(t),$
and by the chain rule,
$$ x'(t) = \frac{dx}{dt} dt, \quad y'(t) = \frac{dy}{dt} dt. $$
Therefore,
$$ z'(t) = \frac{dz}{dt} = \frac{dx}{dt} + i \frac{dy}{dt} $$
or equivalently
$$ dz = z'(t) dt. $$
Then we have
$$ \int_C f(z) dz = \int_\alpha^\beta f[z(t)] z'(t) dt. $$
Referenced by (2 direct)
One trick we can use is that when the modulus of a function is constant, we can use the argument of $z$ as a parameter by writing $C: z = e^{\theta i}, \arg{\alpha} \le \theta \le \arg{\beta}$
When the path of integration in a contour integral is a closed curve, we place a circle on the integral sign
$$ \oint_C f(z) dz. $$
You can add an arrow to the circle to indicate clockwise vs counterclockwise direction, but that's not supported in MathJax so I don't have it here!
Some additional properties:
$$ \Re \int_C f(z) dz = \int_C \Re[f(z)dz]; $$
$$ \Im \int_C f(z) dz = \int_C \Im[f(z)dz]; $$
$$ \left | \int_C f(z) dz \right | \le \int_C |f(z)||dz| \le ML $$
where $M$ is the maximum value of $\|f(z)\|$ for $z$ on $C$, and $L$ is the length of $C$.
Here's an example problem: evaluate $\oint_C e^z dz$ where $C$ is the closed (triangular) path from $0$ to $1$ ($C_1$) to $1 + i$ ($C_2$) back to $0$ ($C_3$):
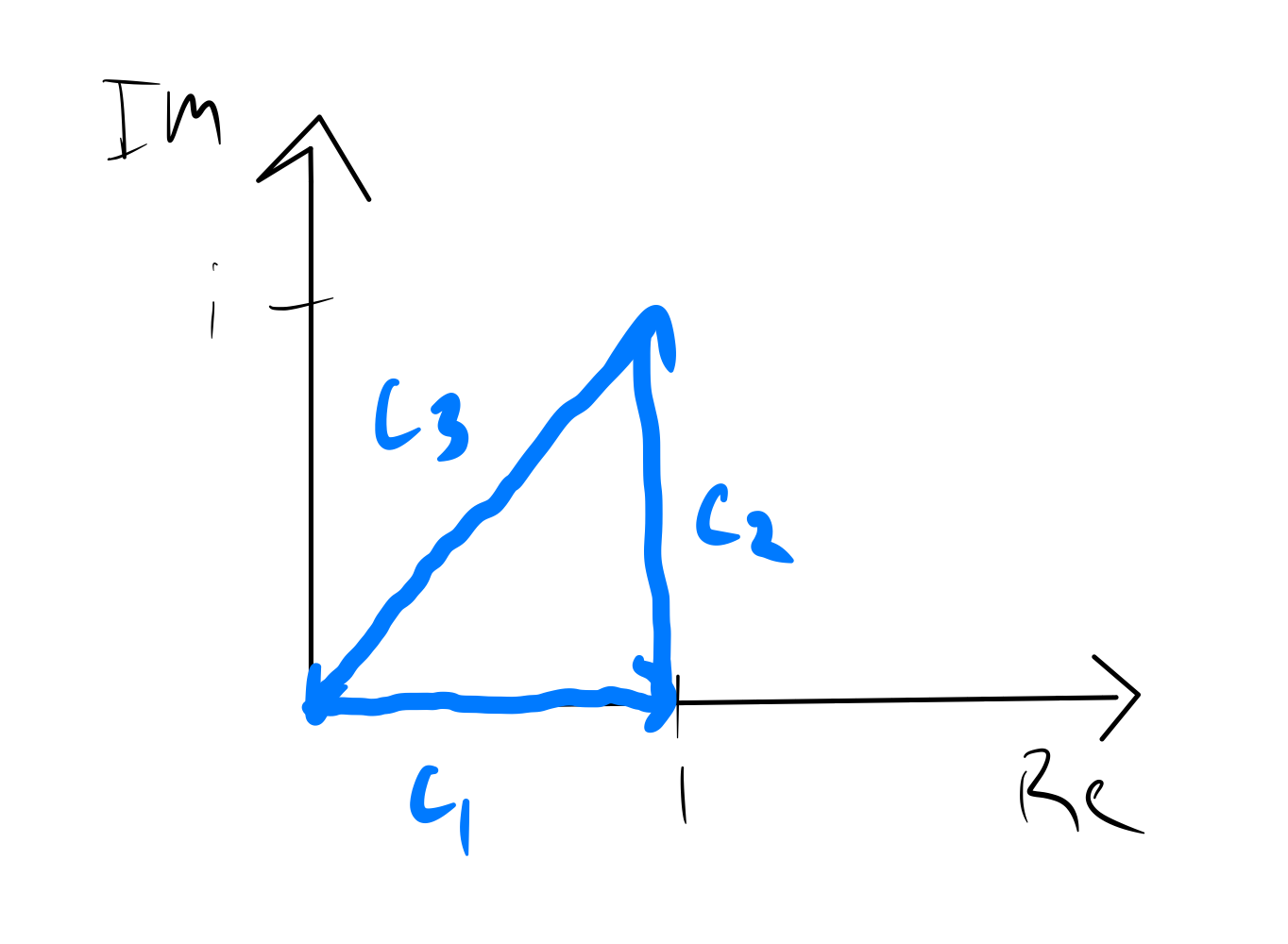
$$ \oint_C e^z dz = \int_{C_1} e^z dz + \int_{C_2} e^z dz + \int_{C_3} e^z dz, $$
where
$$ C_1: y = 0, 0 \le x \le 1; $$
$$ C_2: x = 1, 0 \le y \le 1; $$
$$ C_3: x = t, y = t, 1 \ge t \ge 0; $$
Thus,
$$ \oint_C e^z dz = \int_0^1 e^x dx + \int_0^1 e^{1+yi}idy + \int_1^0 e^{t+ti} (dt +dt~i) $$
$$ = \left \{ e^x \right \}^1_0 + \left \{ e^{1+yi} \right \}^1_0 + \left \{ e^{(1+i)t} \right \}^0_1 $$
$$ = (e - 1) + (e^{1+i} -e) + (1 - e^{1 +i}) = 0. $$
Some Important Contour Integrals
First, we'll compute $\oint_C \frac{1}{z} dz$ where $C$ is the unit circle. We'll call this out as a theorem, because it's a super important result that gets used all the time in complex analysis.
If $C$ is the unit circle, then $ \int_C \frac{1}{z} dz = 2 \pi i.$
First, note that we can parameterize $C,$ the unit circle, as
$$ z(\theta) = e^{i\theta}, 0 \leq \theta < 2 \pi. $$
Now, making the substitution,
$$ f(z(\theta)) = \frac{1}{e^(i\theta)} = e^{-i\theta}. $$
Now, using the definition of the contour integral,
$$ \int_C f(z) dz = \int_\alpha^\beta f[z(t)]z'(t) dt $$
we have, noting that $z'(\theta) = i e^{i \theta},$
$$ \int_C \frac{1}{z} dz = \int_{0}^{2 \pi} e^{-i \theta} i e^{i \theta} d \theta = i \int_{0}^{2 \pi} d \theta = 2 \pi i. $$
$\square$